Cyclomatic complexity
It is the complexity calculated based on the number of paths through the code.
Every program encompasses statements to execute in order to perform some task and other decision-making statements that decide, what statements need to be executed. These decision-making constructs change the flow of the program.
The metric itself is based on graph measures on the control flow graph of a method and describes the non-linearity of this graph. For structured programming the metric is roughly equivalent to one plus the number of loops and if statements. The decision-making constructs used to create the graph model are IF-ELSE, DO-WHILE, WHILE, FOR, TRY-CATCH, GOTO, $CASE and $SELECT statements, and postconditionals like GOTO:pc, SET:pc, etc.
Each function has a minimum complexity of 1.
If we compare two programs of same size, the one with more decision-making statements will be more complex as the control of program jumps frequently.
Method of calculation
Process to make flow control graph:
- Break program in smaller blocks, delimited by decision-making constructs.
- Create nodes representing each of these nodes.
- Connect nodes as follows:
- If control can branch from block i to block j ⇒ Draw an arc
- From exit node to entry node ⇒ Draw an arc
To calculate Cyclomatic complexity of a program module, we use the formula
V(G) = e – n + 2
Where
e is total number of edges
n is total number of nodes
Check the next example:
|
Code |
Flow Chart |
Flow Graph |
||
 |
→
|
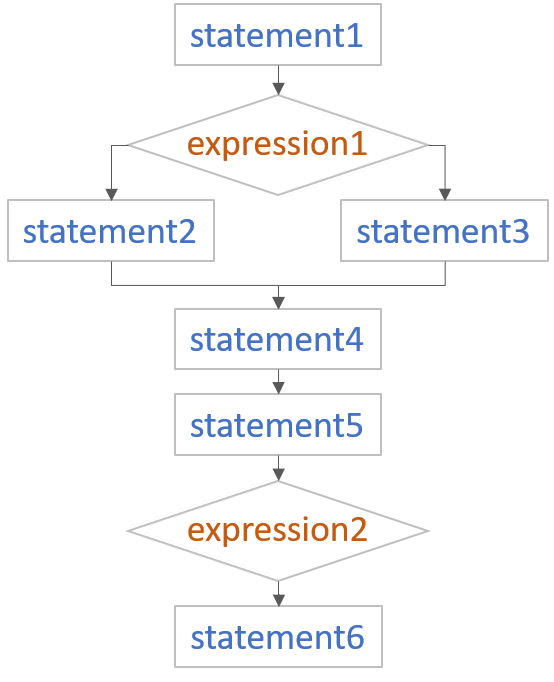 |
→
|
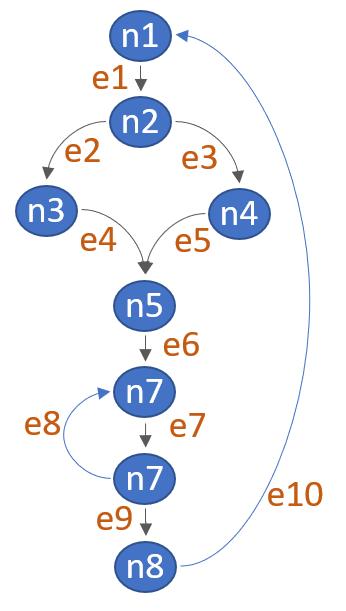 |
The Cyclomatic complexity of the above module is
e = 10
n = 8
Cyclomatic Complexity = 10 - 8 + 2
= 4
History
Cyclomatic Complexity is a metric that was introduced by Thomas McCabe in 1976 and aims at capturing the complexity of a method in a single number.
Actually, the original publication talks about the more general term module, but today this typically means function or method for most languages.

